LIBS Info: Understanding: Are all LIBS peaks self-absorbed?
Are all LIBS peaks self-absorbed?
Short Answer: Yes, but there are order of magnitude differences in the effect depending on the energy of the lower level in the transition.
Long Answer: Self absorption refers to the effect where light emitted by an element in a LIBS plasma is absorbed by that element in another part of the plasma. This leads to a pronounced 'flattening' of a plot of peak intensity vs concentration, as in the image below.
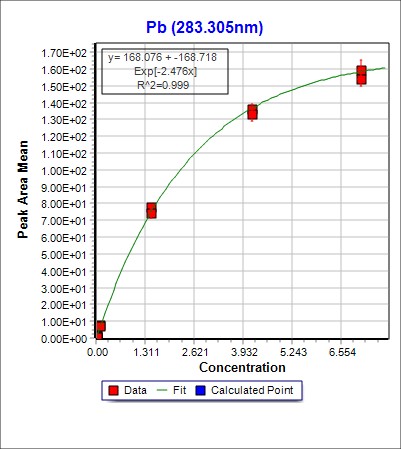
While the lower concentration region of the calibration curve is still usable, at higher concentrations the uncertainty in the intensity leads to an unacceptably large uncertainty in the concentration.
The full expression for the peak intensity (see, for example Yaroshchyk etal. ) is given by $$\begin{aligned} I = \alpha \frac{8 \pi h c}{\lambda^3} e^{\frac{-(E_k - E_i)}{kT}} \left ( 1-exp\left [ -\frac{\sqrt{ln2}}{4 \pi \sqrt{\pi}} \frac{\lambda^2}{\Delta \nu_D} \frac{g_k A_{ki} N}{U(T)} e^{\frac{-E_i}{kT}} K(a,x)) \right ] l \right ) \end{aligned} $$ where $$\begin{aligned} I &=Intensity \\ \alpha &=scaling\quad factor \\ T &=temperature \\ U(T) &= partition\quad function \\ A_{ki} &= Einstein \quad Coefficient \quad for \quad the \quad transition \\ g_{k} &= Lower\quad level \quad degeneracy \\ E_{k} &= Upper\quad level \quad energy \\ E_{i} &= Lower\quad level \quad energy \\ k &=Boltzmann's \quad constant \\ \Delta \nu_D &= Doppler \quad linewidth\\ N &= Number \quad of \quad atoms \quad of \quad the \quad element \\ K &= Lineshape \\ l &= absorption \quad path \quad length \quad (that \quad is, \quad plasma \quad size) \end{aligned} $$ collecting together constants gives: $$ \begin{aligned} I = X e^{\frac{-(E_k - E_i)}{kT}} \left ( 1-exp\left [ Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}} \right ] \right ) \end{aligned} $$ where we are using C for concentration of the element.
Using the Taylor expansion: $$ \begin{aligned} e^x = \sum _{n=1}^\infty \frac{x^n}{n!} \end{aligned} $$ gives $$\begin{aligned} I &= X e^{\frac{-(E_k - E_i)}{kT}} \left ( 1-\left [1- Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}} + \frac {1}{2} \left ( Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}}\right)^2 - \frac {1}{3!} \left ( Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}}\right)^3... \right ] \right ) \end{aligned} $$ $$\begin{aligned} = X e^{\frac{-(E_k - E_i)}{kT}} \left ( Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}} - \frac {1}{2} \left ( Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}}\right)^2 + \frac {1}{3!} \left ( Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_i}{kT}}\right)^3...\right ) \end{aligned} $$ $$\begin{aligned} =X Y \frac{g_k A_{ki} C}{U(T)} e^{\frac{-E_k}{kT}} - e^{\frac{-E_k}{kT}} e^{\frac{-E_i}{kT}}\left [ \frac {X}{2} \left ( Y \frac{g_k A_{ki} C}{U(T)} \right)^2 - \frac {1}{3!} \left ( Y \frac{g_k A_{ki} C}{U(T)} \right)^3 e^{\frac{-2E_i}{kT}} ...\right ] \end{aligned} $$ The key things to note are:-
- The first term is the usual expression for LIBS peak intensity
- The second term, the nonlinear/self-absorption term, is proportional to Ei, the energy of the lower level in the transition.
This makes a level of sense, if we return to the physical explanation of what is happening - light emitted by one part of the plasma (due to transitions from higher energy levels to lower ones) is absorbed by the same elements in another part of the plasma (due to transitions from lower energy levels to higher ones). The effect will be strongest for transitions with the most electrons to do the absorbing.
A paper from Wuhan National Laboratory has proposed another method to reduce self-absorption - by collecting the spectra soon after the laser pulse, the plasma is at its hottest and the population of the ground state is at its lowest.